Modern Automated Theorem Provers
Superposition Calculus
Many modern automated theorem provers, like E, Vampire, SPASS, make use of the superposition calculus.
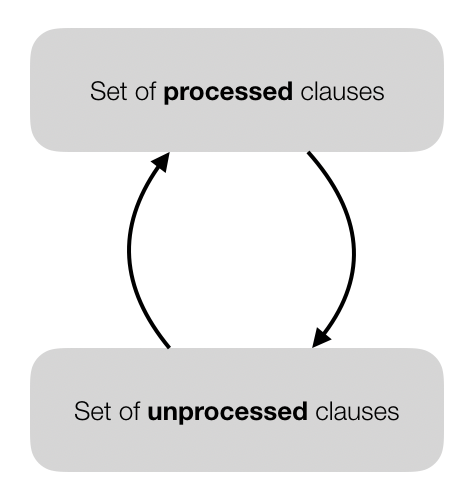
For example, the E theorem prover (invented in 2002) has 2 sets that are growing over time, namely a set of processed and a set of unprocessed clauses. The prover keeps an invariant, viz. the set of processed clauses are the clauses that are processed and no other clauses can be generated from them. At each iteration, an unprocessed clause is selected and compared with all processed clauses. If the algorithm terminates, it is either because an empty clause is found or because no other inferences can be performed. As highlighted by Schulz in 2015, the most important aspect is the selection of clauses in the unprocessed set
Connection Calculus
Connection calculus is another paradigm of calculus. It is goal-driven, meaning that at each stage it is like to start a new proof, and it is not confluent (differently from resolution-based calculi which are not goal-driven and are confluent, because they aim at showing the empty clause). Typically you proceed to negate the statement and prove the unsatisfiability of it. This is obtained if all branches are closed. leanCop is an automated theorem prover based on connection calculus (invented in 2003).
Connection. You have a connection between two clauses if you can find a set $\{A(t_1,\dots,t_n),\neg A(t_1,\dots,t_n)\}$. This is very similar to resolution methods.
The set of inference rules is given by (you should read in bottom-up fashion):
| Name | Rule | Description | Comments |
|---|---|---|---|
| Axiom rule | $\frac{}{\{\},M,PATH}$ | This rule closes a branch | |
| Start rule | $\frac{C_2,M,\{\}}{\epsilon,M,\epsilon}$ | $C_2$ is copy of a clause in M | This rule initiates the tree |
| Reduction rule | $\frac{C,M,PATH\cup\{L_2\}}{C\cup\{L_1\},M,PATH\cup\{L_2\}}$ | $\{\sigma(L_1),\sigma(L_2)\}$ is a connection | This rule just look if the current clause and the path have inconsistent literals (this is similar to the factoring rule) |
| Extension rule | $\frac{C_2\setminus\{L_2\},M,PATH\cup\{L_1\}\quad C,M,PATH}{C\cup\{L_1\},M,PATH}$ | $\{\sigma(L_1),\sigma(L_2)\}$ is a connection | This consider the current clause and compares it with all clauses in M (it is weaker than the resolution rule as it doesn't allow all pair comparisons, namely one clause is fixed to the current clause) |
M is said to be a matrix, namely a set of sets of literals.
When performing extension, the set of comparisons is fixed and it is not growing compared to superposition calculus. This is an important characteristic to consider for applying RL frameworks as the action space does not grow.
Example of proof
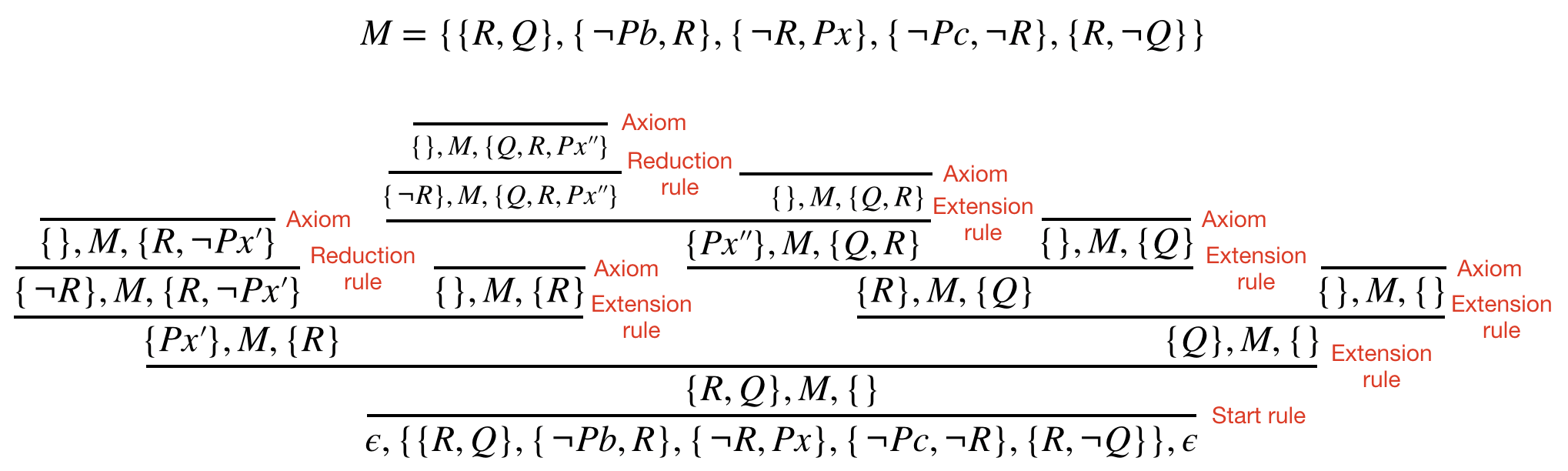
Summary of Automated Theorem Provers
| Calculus | Goal-driven | Confluent | Modern ATPs | Main task for machine learning | Advantage for machine learning |
|---|---|---|---|---|---|
| Superposition (resolution-based) | No | Yes (clauses are leaves and the root is the empty clause) | E, Vampire, SPASS | Selection of pair of clauses for inference | |
| Connection | Yes | No (a starting clause is the root and the goal is to try to close all branch) | leanCOP | Selection of clause based on current one is fundamental to ensure that a branch gets closed in future | The selection is performed from a set that is fixed |
There are other calculi, like the Tableaux calculus
Machine Learning and Automated Theorem Provers
- 2007 MaLARea (Machine Learning for Automated Reasoning). "MaLARea: A Metasystem for Automated Reasoning in Large Theories". Premise selection. First machine learning system using Naive Bayes
- 2011 MaLeCOP. "MaLeCOP Machine Learning Connection Prover". Internal guidance. Using LeanCOP prover and Naive Bayes.
- 2015 FEMaLeCOP. Internal guidance. Improved efficiency of MaLeCOP
- 2016 DeepMath. Premise selection. Using E prover with deep learning
- 2018 "Reinforcement Learning of Theorem Proving". Internal guidance. Using LeanCOP prover with reinforcement learning and Monte Carlo Tree Search

 Email
Email LinkedIn
LinkedIn Twitter
Twitter