Introduction to Reinforcement Learning

Reinforcement Learning (RL) is a paradigm of learning from data (an area of machine learning).

In RL, there are two main components, namely an agent and an environment. These two components interact iteratively over time. On one hand, the environment generates an observation $O_t$ of its state and a reward $R_t$, given an action $A_{t-1}$ chosen by the agent. On the other hand, the agent receives the observation and the reward from the environment and chooses a new action $A_t$. The following picture summarizes the RL paradigm.

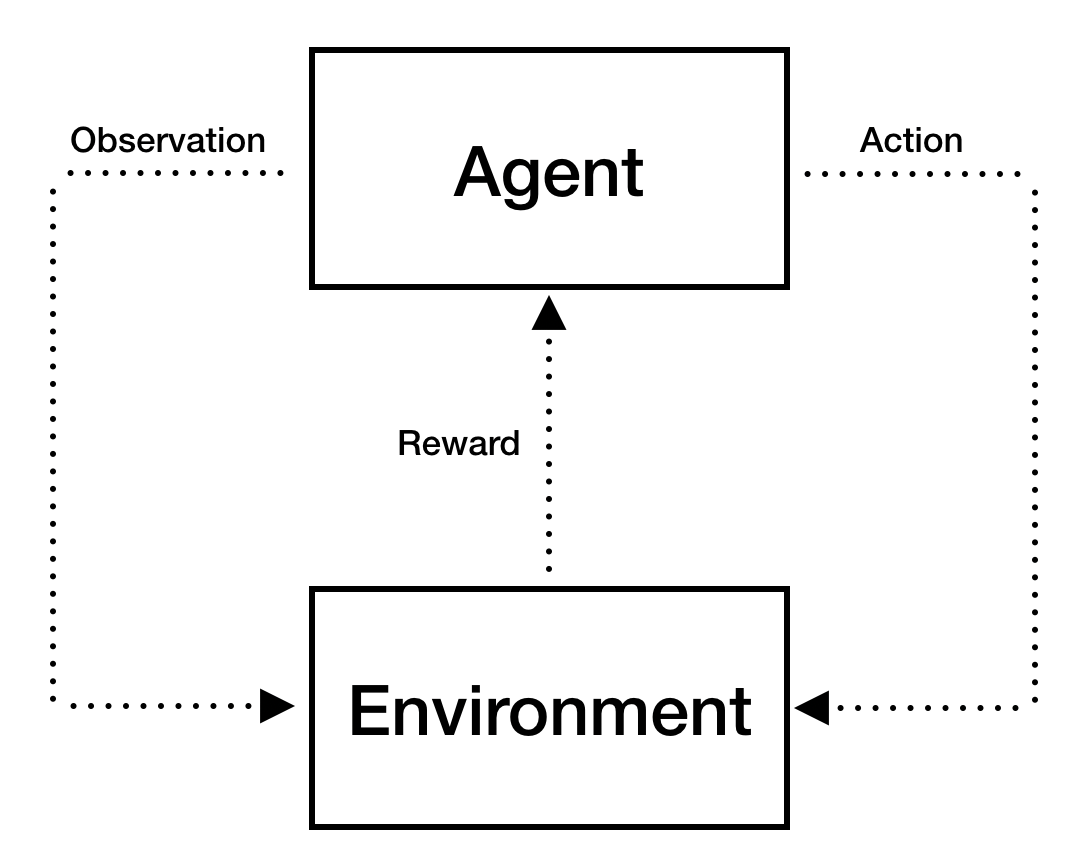
RL is general enough to capture the notion of machine intelligence (see this definition). It is more general than traditional supervised learning, as (i) the supervisory signal (i.e. the reward) is not directly linked to the agent output, (ii) there is no i.i.d. data assumption and (iii) agent actions may affect subsequent data. Thanks to these properties, it is used in a large number of real-world problems involving decision making.

Definitions

Reward. There are two kinds of reward, namely the external reward provided by the environment and the intrinsic reward created by the agent. The external reward comes in many different forms

History. $H_t=O_1,R_1,\dots,A_{t-1},O_t,R_t$

State. A state is a function of the entire history, i.e. $S_t=f(H_t)$. We have the environment state and the agent state.

Note that a state is Markov iff $p(S_{t+1}|S_t)=p(S_{t+1}|S_t,\dots,S_1)$. (if $f(H_t)=H_t$, then it's obvious that the state is Markov. The environment state is by definition a Markov state.)

The environment

The environment performs two actions:

1. Take action. Given $A_{t-1}$ and $S^e_{t-1}$ compute $R_t$ and $O_t$.
2. Update state. Given $A_{t-1},O_t,R_t$ and $S^e_{t-1}$ compute $S^e_t$.

The environment can be

1. Fully observable. Meaning that $O_t=S^e_t$. Therefore, we have a Markov Decision Process
2. Partially observable. Meaning that $O_t\neq S^e_t$. Therefore, we have a Partially Observable Markov Decision Process

The agent

The environment performs two actions:

1. Update state. Given $O_t,R_t$ and $S^a_{t-1}$ compute $S^a_t$.
2. Take action. Given $S^a_t$ compute $A_t$.

In MDP, a good choice for $S^a_t\doteq O_t$. In POMDP, there are different choices:

1. Complete history, $S^a_t=H_t$.
2. Beliefs of the environment, $S^a_t=(P(S^e_t=s_1),\dots,P(S^e_t=s_n))$.
3. Recurrent relation, $S^a_t=\sigma(W_sS^a_{t-1}+W_oO_t)$.

The agent can have some of the following components:

1. Policy.
2. Value function.
3. Model.

Policy

It defines the agent's behaviour. It can be deterministic, viz. $A_t=\pi(S^a_t)$. Or it can be stochastic, viz. $\pi(a|s)=P(A_t=a|S^a_t=s)$.

Value function

Prediction of future reward for a given policy $\pi$. For example, $v_\pi(s)=E_\pi\{R_{t+1}+\gamma R_{t+2}+ \gamma^2 R_{t+3} + \dots|S_t=s\}$.

Model

It predicts what the environment will do next. Typically, you learn a transition model and a reward model.

Taxonomy of RL agent

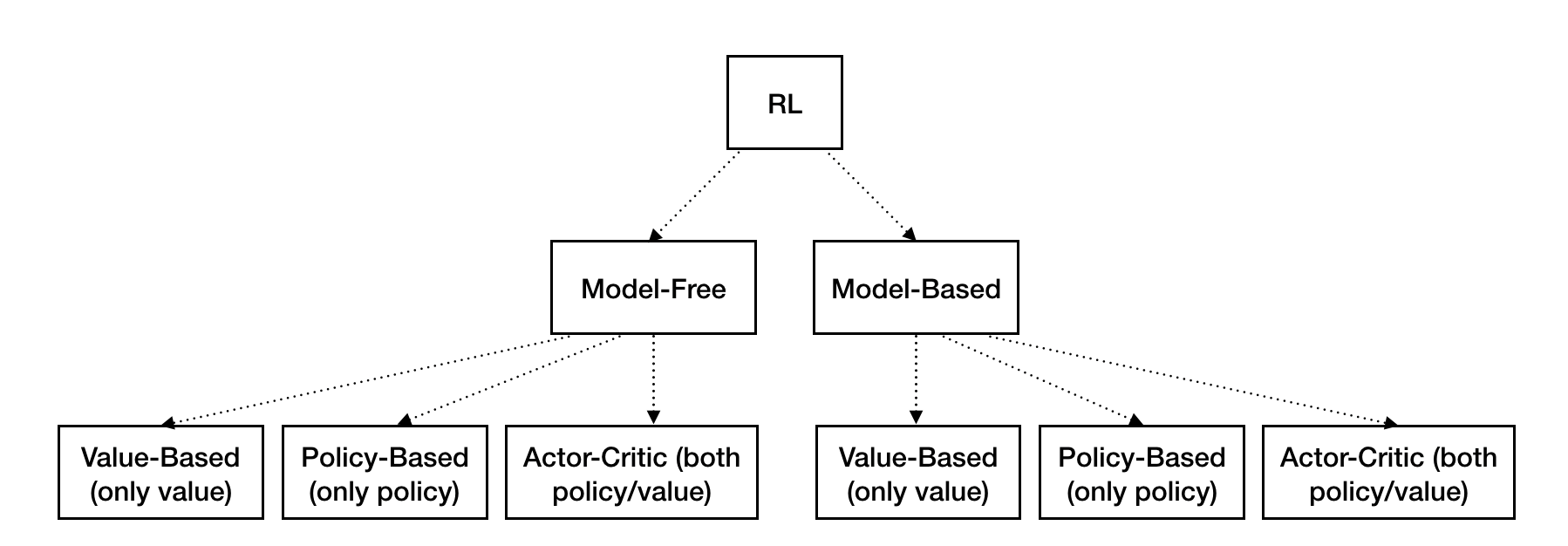
Problems within RL

The environment is initially unknown and the agent must learn through interaction. One way to do reinforcement learning is to first learn the model of the environment, and then plan. Therefore, the planning problem starts from the assumption that the model is known.

Two main problems:

1. Prediction. Given a policy, compute the value function
2. Control. Find the best policy