Model-Free Control

Assumption:

1. unknown MDP. You know the states, but you don't know the transition probabilities and the reward function
2. All states must be visited enough times.

Goal. We want to find the optimal policy.
There are two main strategies, namely on-policy learning (learning by doing) and off-policy learning (learning from someone else's policy)

On-Policy Learning

The main idea is to use Generalized Policy Iteration, which consists of iteratively applying two steps, viz. policy evaluation (computing the value of a policy) and policy improvement.

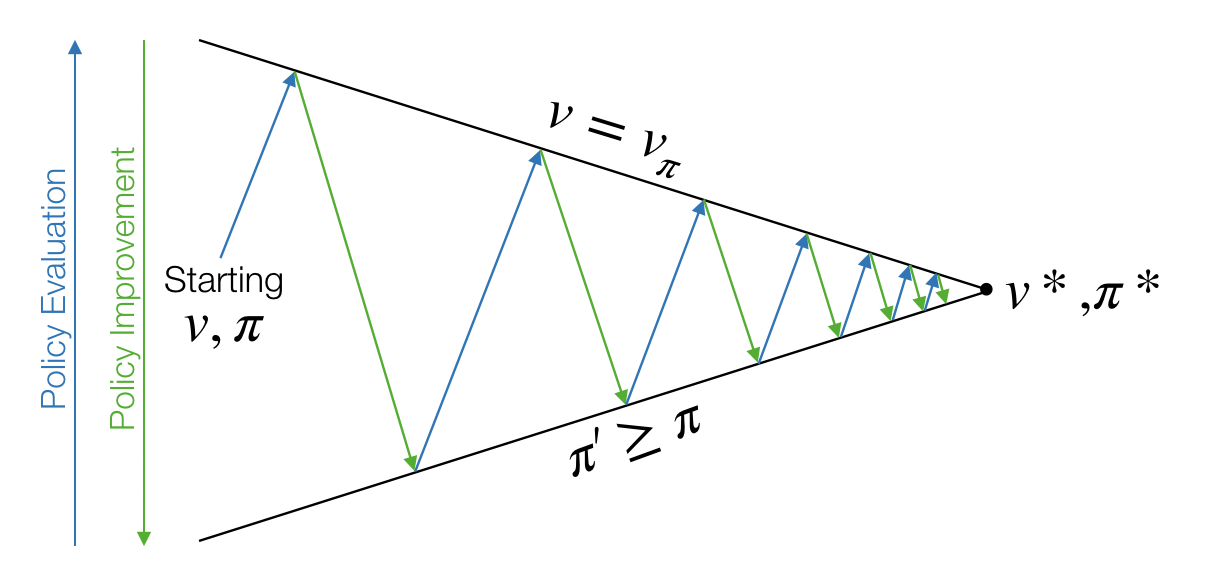
On-Policy - Trial 1: Generalized Policy Iteration with Monte-Carlo Evaluation

Policy Evaluation Monte-Carlo policy evaluation on state-value function.
Policy Improvement Greedy policy improvement $\pi(s)=\arg\max_a R_s^a + \gamma\sum_{s'}P_{ss'}^a v(s')$.

Problem 1. This solution is not model-free. You need $P$.
Problem 2. Deterministic policy has issues about exploration.

On-Policy - Trial 2: Generalized Policy Iteration with Action-Value Function

If you use the action-value function, you can do control without needing the model

Policy Evaluation Monte-Carlo policy evaluation on action-value function.
Policy Improvement Greedy policy improvement $\pi(s)=\arg\max_a q(a,s)$.

Problem 2. Deterministic policy has issues about exploration.
Consider a case with two possible actions. One of them gives small reward at each timestep, while the other one gives huge and rare rewards. A greedy policy always selects the action with small and frequent reward, but it's not guaranteed to be optimal.

On-policy - Trial 3: Monte-Carlo Policy Iteration

Policy Evaluation Monte-Carlo policy evaluation on action-value function.
Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q_\pi(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Theorem. $\epsilon$-greedy exploration improves the policy, namely $v_{\pi'}(s)\geq v_\pi(s)$.
Proof. $$\begin{align} \sum_{a}\pi'(a|s)q_\pi(a,s) &= (1-\epsilon)\max_a q_\pi(a,s) + \frac{\epsilon}{m}\sum_a q_\pi(a,s) \\ &\geq (1-\epsilon)\sum_a \pi^{''}(a|s) q_\pi(a,s) + \frac{\epsilon}{m}\sum_a q_\pi(a,s) \quad\text{where}\quad \pi^{''}(a|s)=\frac{\pi(a|s)-\epsilon/m}{1-\epsilon} \\ &= (1-\epsilon)\sum_a \frac{\pi(a|s)-\epsilon/m}{1-\epsilon}q_\pi(a,s) + \frac{\epsilon}{m}\sum_a q_\pi(a,s)\\ &= \sum_{a}\pi(a|s)q_\pi(a,s) \end{align}$$ QED

Problem. This is a bit inefficient, because we evaluate a policy on multiple episodes. If the policy is bad, we spend too much time on evaluating that bad policy.

On-policy - Trial 4: Monte-Carlo Control

Same as Monte-Carlo Policy Iteration but you evaluate the policy on just a single episode.

Policy Evaluation Monte-Carlo policy evaluation on action-value function on single episode. $q(a,s)\approx q_\pi(a,s)$.
Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Problem. Note that policy evaluation is performed on a single episode (and not an infinite set of episodes), which obtains only an approximation of the action-value function. The subsequent policy improvement is based on this estimation. Are we guaranteed to find the optimal policy?

On-policy - Solution 1: GLIE Monte-Carlo Control

In order to ensure convergence to the optimal policy, we need to satisfy two conditions:

GLIE (Greedy in the Limit of Infinite Exploration).

1. All state-action pairs must be explored infinitely many times (in order not to discard any of them), namely $\lim_{t\rightarrow\infty}N_t(a,s)=\infty$.
2. The final policy must be greedy (deterministic), $\lim_{t\rightarrow\infty}\pi_t(a|s)=1[a=\arg\max_{a'}q_t(a',s)]$.

Note that the GLIE property can be ensure by choosing $\epsilon=1/t$.

Policy Evaluation Monte-Carlo policy evaluation on action-value function on single episode.

$$\begin{align}\text{for each pair of state,} & \text{ action in the episode} \\ & N(A_t,S_t)=N(A_t,S_t)+1 \\ & q(S_t,A_t)=q(S_t,A_t) + \frac{1}{N(A_t,S_t)}\big(G_t-q(S_t,A_t)\big)\end{align}$$

Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Choose $\epsilon=1/t$.

Theorem. GLIE Monte-Carlo control converges to the optimal action-value function as long as the number of collected episodes is large enough, namely $q(A_t,S_t)\rightarrow q^*(A_t,S_t)$ for $t\rightarrow\infty$.
Proof. NOT HERE

On-policy - Solution 2: Control with Sarsa

We want to have an online algorithm.
Recall that MC policy evaluation uses $q(S_t,A_t)=q(S_t,A_t) + \alpha\big(G_t-q(S_t,A_t)\big)$. Then, we can replace $G_t$ with the TD target $R_{t+1}+\gamma q(S_{t+1},A_{t+1})$ and obtain Sarsa. (In fact, recall that $q_\pi(a,s)=R_s^a+\gamma\sum_{s'}P_{ss'}^a\sum_{a'}\pi(a'|s')q_\pi(a',s')$).

Policy Evaluation online policy evaluation on action-value function.

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\big(R_{t+1}+\gamma q(S_{t+1},A_{t+1})-q(S_t,A_t)\big)$$

Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore $$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$ Choose $\epsilon=1/t$.

Theorem. Assume that

1. We have GLIE policies
2. The sequence of $\alpha_t$ satisfies the Robbins Monro conditions:
   1. $\sum_{t=1}^\infty \alpha_t = \infty$ (meaning that we are able to move our estimate $q(s,a)$ wherever we want).
   2. $\sum_{t=1}^\infty\alpha_t^2<\infty$ (meaning that the changes eventually diminish).

Then, Sarsa converges to optimal action-value function.
Proof. NOT HERE
Question. Can we unify the last two solutions?

On-policy - Solution 3: Control with n-Step Sarsa

We can replace $G_t$ with the n-step TD target $q_t^{(n)}=R_{t+1}+\gamma R_{t+2} + \dots + \gamma^{n}q(S_{t+n},A_{t+n})$

Policy Evaluation policy evaluation on action-value function

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\big(q_t^{(n)}-q(S_t,A_t)\big)$$

Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Choose $\epsilon=1/t$.

Question. Which $n$ is the best?

On-policy - Solution 4: Control with Sarsa($\lambda$)

Combine all $n$

Policy Evaluation policy evaluation on action-value function.

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\big(q_t^{\lambda}-q(S_t,A_t)\big)$$
where $q_t^{\lambda}=(1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}q_t^{(n)}$.

Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Choose $\epsilon=1/t$.

Question. How to make it online?

On-policy - Solution 5: Control with Online Sarsa($\lambda$)

Define an eligibility trace, namely:

$$E_0(a,s)=0$$
$$E_t(a,s)=\gamma\lambda E_{t-1}(a,s) + 1[S_t=s, A_t=a]$$

Then,

Policy Evaluation policy evaluation on action-value function.

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\delta_tE_t(S_t,A_t)$$

where $\delta_t=R_{t+1}+\gamma q(S_{t+1},A_{t+1})-q(S_t,A_t)$.
Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\pi'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Choose $\epsilon=1/t$.

Off-Policy Learning

We have a behaviour policy $\mu$ (the one which really acts in the environment) and a target policy $\pi$, which we want to know its state-value function.
Why?

1. The behaviour policy can be from other agents (e.g. humans)
2. Re-use experience from old policies
3. Following exploratory policy and learn the optimal one
4. Follow one policy and learn multiple ones

Importance sampling. Imagine you have 2 distributions $P$ and $Q$. Then

$$\begin{align}E_{X\sim P}\{f(X)\} &= \sum P(X)f(X) \\ &= \sum P(X)\frac{Q(X)}{Q(X)}f(X) \\ &= \sum Q(X)\bigg(\frac{P(X)}{Q(X)}f(x)\bigg) \\ &= E_{X\sim Q}\bigg\{\frac{P(X)}{Q(X)}f(x)\bigg\}\end{align}$$

The quantity we want to estimate is $G_t$.

Trial 1: Off-Policy Monte Carlo

We take actions using $\mu$ and we estimate $G_t$ by importance sampling over the actions.

$$\begin{align}G_t^{\pi/\mu} &= \frac{\pi(A_t,A_{t+1},\dots,A_T|S_t,S_{t+1},\dots,S_T)}{\mu(A_t,A_{t+1},\dots,A_T|S_t,S_{t+1},\dots,S_T)}G_t \\ &=\frac{\pi(A_t|S_t,S_{t+1},\dots,S_T)\pi(A_{t+1}|S_t,S_{t+1},\dots,S_T)\dots\pi(A_T|S_t,S_{t+1},\dots,S_T)}{\mu(A_t|S_t,S_{t+1},\dots,S_T)\mu(A_{t+1}|S_t,S_{t+1},\dots,S_T)\dots\mu(A_T|S_t,S_{t+1},\dots,S_T)}G_t \\ &=\frac{\pi(A_t|S_t)\pi(A_{t+1}|S_{t+1})\dots\pi(A_T|S_T)}{\mu(A_t|S_t)\mu(A_{t+1}|S_{t+1})\dots\mu(A_T|S_T)}G_t\end{align}$$

and the update is

$$v(S_t)=v(S_t)+\alpha\big(G_t^{\pi/\mu}-v(S_t)\big)$$

The main problem with this algorithm is that the estimator has too high variance!
In practice, Monte Carlo is never used for off-policy learning.

Solution 1: Off-Policy Temporal Difference

We take actions using $\mu$ and we estimate $G_t$ by importance sampling over the actions.

$$G_t^{\pi/\mu}=\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}\big(R_{t+1}+\gamma v(S_{t+1})\big)$$

and the update is

$$v(S_t)=v(S_t)+\alpha\big(G_t^{\pi/\mu}-v(S_t)\big)$$

This solution has much less variance compared to off-policy MC.

Solution 2: General Q-Learning

We don't need to use importance sampling. In fact, we can use a behaviour policy $\mu$ to act in the environment. And we update the TD target using an alternative action from target policy $\pi$.

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\big(R_{t+1}+\gamma q(S_{t+1},A_{t+1})-q(S_t,A_t)\big)$$

where $A_{t+1}=\arg \max_a q(S_{t+1},a)$ (from policy $\pi$). Therefore,

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\big(R_{t+1}+\gamma \max_a q(S_{t+1},a)-q(S_t,A_t)\big)$$

Solution 3: Special case of Q-Learning (Sarsa MAX)

Here, we have a special case of Q-Learning. Case where we want learn a greedy behaviour following an explorative behaviour. In fact, behaviour policy $\mu$ is $\epsilon$-greedy, while the target policy $\pi$ is greedy.

Policy Evaluation policy evaluation on action-value function.

$$q(S_t,A_t)=q(S_t,A_t) + \alpha\big(R_{t+1}+\gamma \max_a q(S_{t+1},a)-q(S_t,A_t)\big)$$

Policy Improvement $\epsilon$-Greedy exploration, namely choose greedy action with probability $1-\epsilon$ or choose all other actions with probability $\epsilon$. Therefore

$$\mu'(a|s)=\left\{\begin{array}{ll} 1-\epsilon+\frac{\epsilon}{m} & if a=\arg\max_{a'}q(a',s) \\ \frac{\epsilon}{m} & otherwise \end{array}\right.$$

Theorem. Sarsa MAX converges to optimal action-value function. (In fact, it fulfills the GLIE property)
Proof. NOT HERE