Model-Based RL

Here is the summary of the lecture

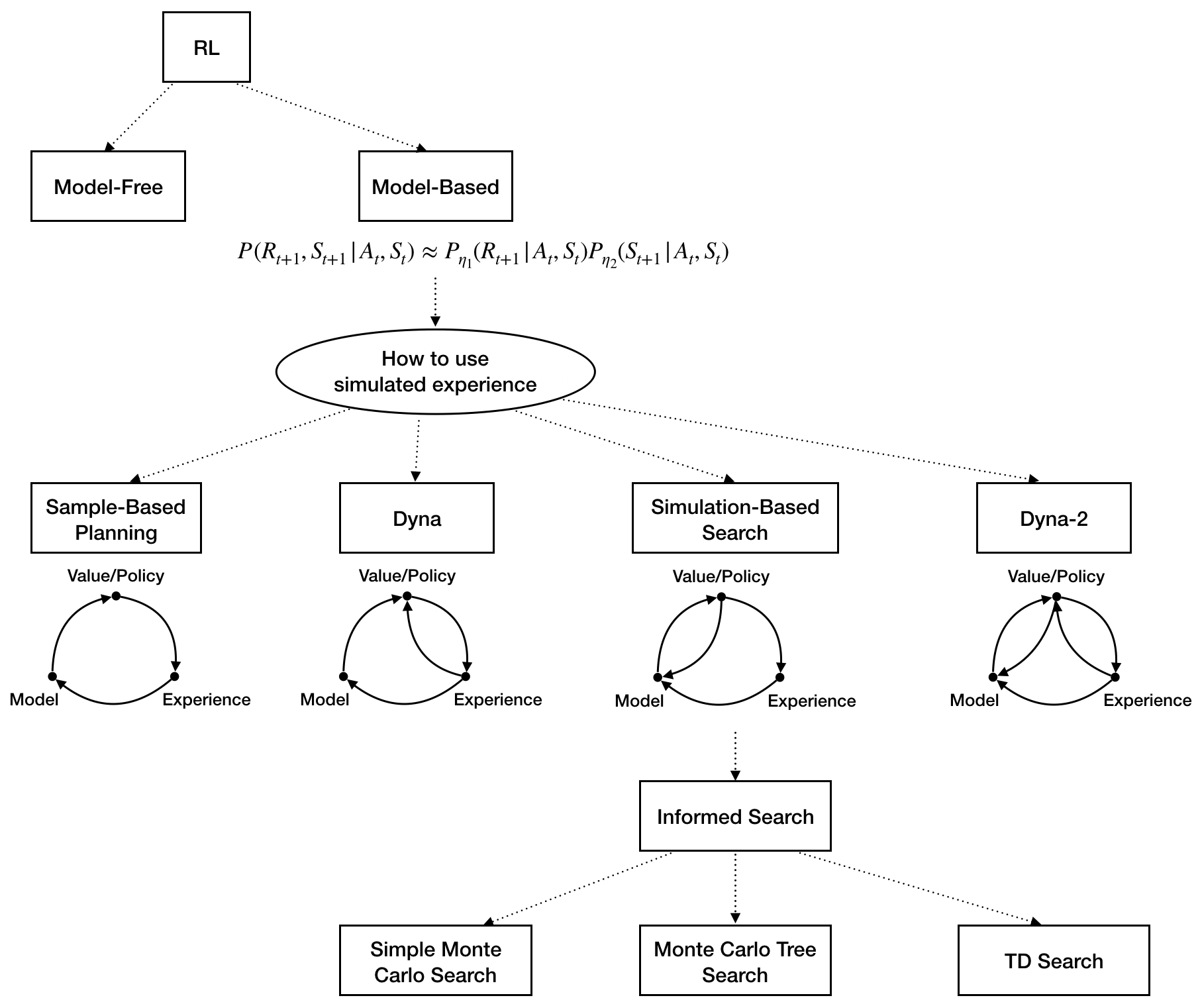
Model-based

The paradigm of model-based RL is to learn a parameterized model which can be easily trained through supervised learning and can be used to generate experience. There are two reasons to prefer model-based over model-free RL:

Training a model is in general easier than learning an action-value function (in fact, it is easier to learn the reward for a state-action pair than learning the return for a state-action pair). Arguably, you can use policy gradient algorithms.
If the learnt model is good, then you can sample a experience from it, thus learning more efficiently.

Typically, we assume conditional independence between the reward and the next state, namely

$$P(R_{t+1},S_{t+1}|A_t,S_t)=P(R_{t+1}|A_t,S_t)P(S_{t+1}|A_t,S_t)$$

Therefore, the model approximates the two conditional densities.

$$\begin{align} P(R_{t+1}|A_t,S_t)&\approx P(R_{t+1}|A_t,S_t,\eta_1) \\ P(S_{t+1}|A_t,S_t)&\approx P(S_{t+1}|A_t,S_t,\eta_2) \end{align}$$

Different models can be used, namely:

Nonparametric table lookup, viz. store tuples $<S_t,A_t,R_{t+1},S_{t+1}>$
Table lookup, viz. estimate $P_{ss'}^a$ and $R_s^a$ for all $s,a,s'$.
Linear models
Nonliner models

IT'S IMPORTANT TO LEARN A GOOD MODEL (PROBLEM OF LEARNING A MODEL). Once we have a model, we can generate experience. But, how can we exploit the sampled experience? (PROBLEM OF USING SAMPLED EXPERIENCE)

How to Use Simulated Experience

A natural way to exploit the sampled experience is to use model-free RL. Here, we provide the pseudo-code for the most-general algorithm


      1. s <- initial state
      2. Initialize Model M
      3. Initialize policy/value functions
      4. loop until termination
      5.    a <- Act in the real world
      6.    r <- get reward
      7.    s' <- sample next state
      8.    Learn policy/value functions on real experience (s,a,r,s')
      9.    Update model M based on s,a,r,s'
      10    Sample experience from model M and learn policy/value functions on simulated experience (MODEL-FREE RL)
      11    s <- s'

In the pseudo-code there are two ways to learn policy/value functions. We can use either real experience or simulated experience or both. Furthemore, we can use different strategies to sample simulated experience. All these degrees of freedom allow to specify a wide variety of RL algorithms. In the next subsections, we overview some of them.

Sample-Based Planning

In sample-based planning we don't learn from real experience (no line 8 in the pseudo code). Furthermore, the sampling of experience from model M is performed in a random way (random states, random actions).

Dyna

In Dyna, we learn from both real and simulated experience. Furthermore, the sampling of experience from model M is performed in a random way (random states, random actions from previous observed ones). Dyna-Q combines model-based and value-based RL (viz. using the action-value function).

Simulation-Based Search

In simulation-based search we learn only from simulated experience. The main difference with respect to previous cases lies in the sampling of experience. Instead of sampling randomly, we condition on the current state and we perform a search for the most promising experiences. Practically speaking, the differences consists of (i) setting the initial state of each simulated experience to the current one instead of choosing it randomly and (ii) using a simulation policy instead of a random one, to guide the search.

THE PROBLEM OF USING SIMULATED EXPERIENCE, IN PARTICULAR THE PROBLEM OF SAMPLING, IS CONVERTED TO A SEARCH PROBLEM (IN A TREE).

In general, there are different ways to perform search. There are classical approaches, based on uninformed search (e.g. breadth-first search, depth-first search) or informed search (e.g. best-first search, $A^*$ search), and non classical ones, based for example on adversarial search. For more details, please see the book of Russell and Norvig. In this subsection, we focus on best-first search strategies.

Simple Monte-Carlo Search

In simple Monte-Carlo search, line 10 in the pseudo-code is specified as follows:

Given fixed simulation policy
      a.    for each action a
      b.        sample K episodes of experience using the fixed policy based on initial state s and action a
      c.        Q(s,a) <- Monte-Carlo estimate on K episodes

Characteristics:

Simulation policy is fixed
The action-value function is estimated for all actions, but only for the current state
At each iteration of the for loop (line 4 in the pseudo-code), the action-value function is re-estimated

Monte-Carlo Tree Search

Monte-Carlo tree search modifies the first two characteristics of simple Monte-Carlo search. The main idea is to incrementally update the simulation policy at each episode. Furthermore, the action-value function is estimated for a subset of states and actions (namely those ones close to the root). Line 10 in the pseudo-code is specified as follows:


      a. Initialize tree by setting the root to current state
      b. for K
      b.    Selection: traverse tree using tree policy (e.g. epsilon-greedy using estimated action-value function) until reaching an unexplored action a (leaf)
      c.    Expansion: expand the tree with state s' sampled from model M (from last visited state s and unexplored action a)
      d.    Rollout: take actions using rollout policy (e.g. random policy) until termination of episode
      e.    Backup: update all state-action pairs involved in the episode contained in the tree using Monte-Carlo estimate

Characteristics:

Simulation policy consists of tree and rollout policy (the idea is to behave randomly in new cases)
Simulation policy changes at each episode
The action-value function is estimated for a subset of actions and states (namely those ones contained in the tree)
At each iteration of the for loop (line 4 in the pseudo-code), the action-value function is re-estimated

The drawback of this method is that it is high variance.

TD Search

To reduce variance, you can update the action value function at each time step of each episode.
Characteristics:

Simulation policy changes at each step of each episode

The drawback is that it has higher bias. Therefore, we can use TD($\lambda$) search.

Dyna-2

We learn from both real and simulated experience. In particular, we combine TD learning on real experience and TD($\lambda$) search on simulated experience. For more details, check 2008 paper.

Summary

Name	Learning from real experience	Sampling (initial state)	Sampling (simulation policy)	Update value/policy	Bias	Variance
Sample-based planning	No	Random	Random	Each real action	Low	Very High
Dyna	Yes	Random	Random	Each real action	Low	Very High
Simulation-based search (Simple Monte-Carlo)	No	Current state	Fixed simulation policy	Each real action	Low	High
Simulation-based search (Monte-Carlo Tree Search)	No	Current state	simulation policy (tree and rollout policies)	Each simulated episode	Low	Medium
Simulation-based search (TD Search)	No	Current state	simulation policy	Each step of simulated episode	Medium	Low
Simulation-based search (TD($\lambda$) Search)	No	Current state	simulation policy	Each step of simulated episode	Medium/Low (tradeoff)	Medium/Low (tradeoff)
Dyna-2	Yes	Current state	simulation policy (TD($\lambda$) Search)	Each real action	Medium/Low (tradeoff)	Medium/Low (tradeoff)

For more updated reference papers about model-based RL check OPENAI website.

Emanuele Sansone